1 Answer

Mandaputtra · Answer 1 · 2023-07-30T11:15:51+0000

Solution:

Consider the following diagram of the rectangular field:

The perimeter P of a polygon is the sum of its sides, thus we can express the perimeter of the given rectangular field as:

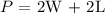
$P\text{ = 2W + 2L }$

where P = 312 yards, L = 83 yards, and L is unknown. Then, replacing the given data into the previous equation, we get:

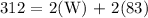
$312\text{ = 2(W) + 2(83)}$

this is equivalent to:

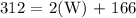
$312\text{ = 2(W) + }166$

solving for 2W, we get:

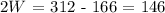
$2W\text{ = 312 - 166 = 146}$

solving for W, we get:

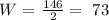
$W\text{ = }(146)/(2)=\text{ 73}$

we can conclude that the correct answer is:

The width of the rectangular field is 73 yards.

Please log in or register to add a comment.