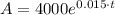Question

Samuel wants to deposit $4.000 and keep that money in the bank without deposits or withdrawals for three years. He compares two different options. Option 1 will pay 1.8% interest, compounded quarterly. Option 2 will pay 1.5% interest, compounded continuously, a How much interest does Option 1 pay? b. How much interest does Option 2 pay?

Answer 1

the Principal P=4000 dollars. The first option pay 1.8% quaterly. In this case, the compounden interest

formula is

`A=P(1+(r)/(4))^(4\cdot t)`

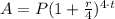
by substituying P=4000 and r=0.018, we have

`\begin{gathered} A=4000(1+(0.018)/(4))^(4\cdot t) \\ A=4000(1.0045)^(0.018\cdot t) \end{gathered}`

hence, in t=3 years, Samuel will have

`\begin{gathered} A=4000(1.0045)^(0.018\cdot3) \\ A=4000.96 \end{gathered}`

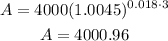
Now, option 2 will pay 1.5 interest, compounded continuously. In this case, the formula is

`A=Pe^(rt)`

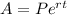
By substituying P=4000 and r=0.015 and t=3, we have

`A=4000e^(0.015\cdot t)`