Question

Hi, I’ve tried getting this question answered but I’m not sure if the app is glitching but my question is not being answered

Answer 1

We are given the following function:

`f(x)=x+8√(7-x)`

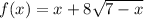
Now, to determine the intervals where the function is increasing we need to determine the first derivative of the function.

`(df)/(dx)=(d)/(dx)(x+8√(7-x))`

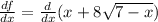
now, we distribute the derivative:

`(df)/(dx)=(d)/(dx)(x)+(d)/(dx)(8√(7-x))`

For the first derivative we use the following rule:

`(d)/(dx)(ax)=a`

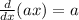
Applying the rule we get:

`(df)/(dx)=1+(d)/(dx)(8√(7-x))`

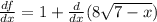
For the second derivative we use the following rule:

`(d)/(dx)(√(f(x)))=((d)/(dx)f(x))/(2√(7-x))`

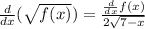
Applying the rule we get:

`(df)/(dx)=1+(-8)/(2√(7-x))`

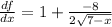
Simplifying we get:

`(df)/(dx)=1-(4)/(√(7-x))`

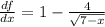
Now, the function is increasing if the derivative is greater than zero. Therefore, we set the following inequality:

`1-(4)/(√(7-x))>0`

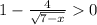
Now, we solve for "x". First, we subtract 1 from both sides:

`-(4)/(√(7-x))>-1`

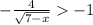
Now, we multiply both sides by -1. Since we multiply by a negative number we change the direction of the inequality:

`(4)/(√(7-x))<1`

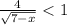
Now, we multiply both sides by the square root of "7 - x":

`4<√(7-x)`

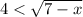
Now, we square both sides:

`16<7-x`

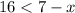
Now, we subtract 7 from both sides:

`\begin{gathered} 16-7<-x \\ 9<-x \end{gathered}`

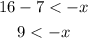
Now, we multiply both sides by -1:

`-9>x`

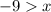
Therefore, the function increases in the interval:

`(-\infty,-9)`

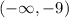
The function must decrease in the other values of the domain. The domain of the function is determined using the fact that the term inside the radical must be always positive. Therefore, we set the following inequality:

`7-x>0`

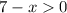
Now, we add "x" to both sides:

`7>x`

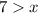
Therefore, the domain of the function is the values of "x" that are smaller than 7. This means that the function must decrease in the interval:

`(-9,7)`