Question

There are 15 marbles in a bag.Two marbles are white, five are blue and eight are red.Find the probability of each event and write your answer as a fraction. I need the steps if possible

Answer 1

Given:

The total number of marbles in the bag, T=15.

The number of white marble, W=2.

The number of blue marbles, B=5.

The number of red marbles, R=8.

The probability of choosing a white marble is,

`P(White)=(W)/(T)=(2)/(15)`

The probability of choosing a blue marble is,

`P(Blue)=(B)/(T)=(5)/(15)=(1)/(3)`

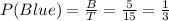
The probability of choosing a red marble is,

`P(Red)=(R)/(T)=(8)/(15)`

The probability of choosing two reds in a row is a dependent event.

There are 8 red marbles in the bag. So, the probability of choosing a red in the first draw is,

`P(\text{ Red in first draw)=}(8)/(15)`

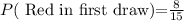
Since one red ball is drawn from the bag, there are only 7 red balls remaining in the bag. Also, there are only 14 balls remaining in the bag. So, the probability of choosing a red in the second draw is,

Now, the probability of choosing two reds in a draw is,