Question

when solving this, do i take it out of the parenthesis or make it into a square root? because its very confusing.

Answer 1

Finding the inverse function:

We are given a function y = f(x). To find the inverse function, we exchange x with y in the original function, and then isolate y.

So

We are given the function:

`f(x)=(x+7)^5`

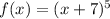
So

`y=(x+7)^5`

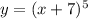
Changing x with y

`x=(y+7_{})^5`

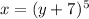
Now, we have to isolate y. So

`(y+7)^5=x`

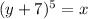
We can apply the fifth root to both sides. So:

`\sqrt[5]{(y+7)^5}=\sqrt[5]{x}`
`y+7=\sqrt[5]{x}`
`f^(-1)(x)=y=\sqrt[5]{x}-7`