Question

Determine the following features of the quadratic function f(x) =-x2 -4x +5

Answer 1

- The quadratic equation given is:

`-x^2-4x+5=f(x)`

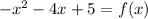
Question 1:

- To know which direction a parabola opens, we follow the these rules:

- The value of a given is -1 < 0.

- Thus, the parabola opens downwards

Question 2:

- The y-intercept of the function is the coordinate of where the graph crosses the y-axis.

- In other words, this is also seen as the point where x = 0. Thus, substituting x = 0 into the equation given to us should readily reveal the y-value of the y-intercept.

- That is,

`\begin{gathered} y=-x^2-4x+5 \\ put\text{ }x=0 \\ y=-0^2-4(0)+5 \\ y=5 \end{gathered}`

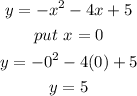
- Thus, the y-intercept is (0, 5)

Question 3:

- The factorization of the function is given below:

`\begin{gathered} f(x)=-x^2-4x+5 \\ \text{ We can rewrite the x-term as follows:} \\ -4x=-5x+x \\ \\ f(x)=-x^2-5x+x+5 \\ \text{ Thus, we can begin to factorize as follows:} \\ f(x)=-x(x+5)+1(x+5) \\ (x+5)\text{ is common so we can factorize again:} \\ \\ f(x)=(x+5)(1-x) \\ \\ f(x)=-1(x-1)(x+5) \end{gathered}`

- Thus, the factorized form is:

`f(x)=-1(x-1)(x+5)`

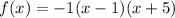
Question 4:

`\begin{gathered} \text{ The vertex of a parabola has its x-coordinate to be:} \\ x=-(b)/(2a)\text{ for the equation: }ax^2+bx+c \\ \\ \text{ Once we have the x-value, we can proceed to find the y-coordinate of the vertex by} \\ \text{ substituting this x-value into the equation.} \\ \text{ We have:} \\ \\ x=-(-4)/(2(-1))=-2 \\ \\ \\ y=-x^2-4x+5 \\ put\text{ }x=-2 \\ y=-(-2)^2-4(-2)+5 \\ y=-4+8+5 \\ y=9 \end{gathered}`

- Thus, the vertex of the parabola is (-2, 9)

Question 5:

- The vertex form of the parabola is given by:

- The equation of the vertex is

`y=-1(x+2)^2+9`