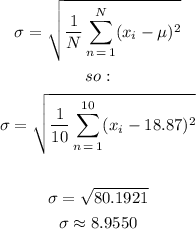The mean is given by:
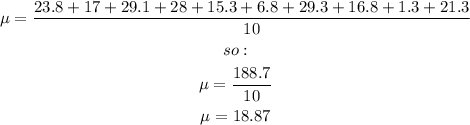
The median is:
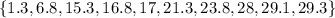
The median is the middle number in a list of values, first we had to sort the list in increasing order. Since we have an even number of values we have to average the middle two numbers, so:
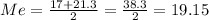
Finally, the standard deviation is: