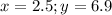ANSWER
Step-by-step explanation
We want to find the x and y components of vector A.
The direction of a vector in the x-y plane is:
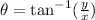
where x = x component; y = y component
Therefore, we have that:
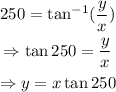
The magnitude of a vector is:
![|A|=\sqrt[]{x^2+y^2}](https://img.qammunity.org/2023/formulas/physics/college/q52bmka5nwjf0w7wkzvsytmivg4atc7eff.png)
Substitute the value of A and y obtained above into the equation:
![7.3=\sqrt[]{x^2+(x\tan250)^2}=\sqrt[]{x^2+x^2\tan ^2(250)}](https://img.qammunity.org/2023/formulas/physics/college/7gv3qv1xtv5lk78qx6x5dsxwq63meyk7mg.png)
Solve for x in the equation:
![\begin{gathered} 7.3^2=x^2(1+\tan ^2(250)) \\ \Rightarrow x^2=(7.3^2)/(1+\tan ^2250) \\ x^2=(53.29)/(1+7.549)=(53.29)/(8.549) \\ x^2=6.2337 \\ \Rightarrow x=\sqrt[]{6.2337} \\ x\approx2.5 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/eroph5381x63e7ndvq4l1h7z0mg9cgw3i3.png)
Recall that:
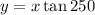
Substitute the value of x:

Therefore, the components are: