Hello there. To solve this question, we'll have to set a system of linear equations and determine how many child tickets were sold that day at the movie theatre.
Given that child admission is $5.40 and adult admission is $9.40, at the movie theatre and knowing that, on friday, 148 tickets were sold for a total of $1171.20, we have to solve for the number of children that attended the movie theatre that day.
First, say the number of children and adults, that friday at the movie theatre, were C and A, respectively.
We know that C + A is the total number of tickets sold.
Multiplying each unknown by the price they paid for the tickets will give us another equation:
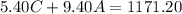
That is, C children paid $5.40 and A adults paid $9.40, for a total of $1171.20.
Hence, we have the following system of linear equations:
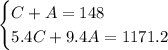
We'll solve for the number of children C using the elimination method.
Multiply the first equation by a factor of 9.4.
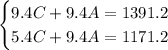
Subtract the second equation from the first, such that we get
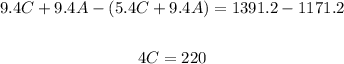
Divide both sides of the equation by a factor of 4
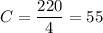
Hence the number of child tickets on friday at the movie theatre was 55.