A plot to illustrate the scenario first.
Given the illustration above, our approach is to find the time it will take the plane from the current destination to the place where the telescope is sited.
The boat travels a distance of 180m at 10 metres per second. Therefore, the travel time is:
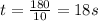
Having found our time, we now find the angle of depression, D since we have the opposite and adjacent sides.
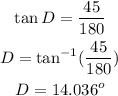
In that case, we can get the rate at which the angle is changing via:
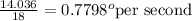
0.7798 degrees per second