Question

Hello! I am in DESPERATE need of help!For the following problem I need to figure out (1.) IF THE LIMIT EXISTS, (2.) IF IT INDICATES THE EXISTENCE OF HORIZONTAL OR VERTICAL ASYMPTOTES, (3.) GIVE THE EQUATION OF SAID ASYMPTOTE, (4.) IF IT APPROACHES NEGATIVE OR POSITIVE INFINTY FROM THE LEFT AND RIGHT. I would HIGHLY appreciate if someone could guide me through the steps for each because I am INCREDIBLY confused!

Answer 1

1. According to the given limit, it is necessary to factor the expressions in numerator and denominator to solve it:

`\begin{gathered} \lim _(x\to6)(x^2-3x+2)/(x^2-x-30) \\ \lim _(x\to6)((x-2)(x-1))/((x-6)(x+5)) \\ \lim _(x\rightarrow6)(4\cdot5)/(0\cdot11) \\ \lim _(x\rightarrow6)(20)/(0)=\infty \end{gathered}`

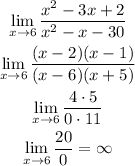
The limit does exist and it is infinite.

2. As the limit when x tends to 6 is infinite, it means there is a vertical asymptote in x=6.

3. The equation of the asymptote is x=6.

4. Evaluate the function in values that close to 6 for example 5.9 and 6.1 to know if it approaches negative or positive infinity from the left and right:

`\begin{gathered} \lim _(x\rightarrow5.9)((5.9-2)(5.9-1))/((5.9-6)(5.9+5)) \\ \lim _(x\rightarrow5.9)((3.9)(4.9))/((-0.1)(10.9))=(19.11)/(-1.09)=-17.53 \\ \lim _(x\rightarrow6.1)((6.1-2)(6.1-1))/((6.1-6)(6.1+5)) \\ \lim _(x\rightarrow6.1)((4.1)(5.1))/((0.1)(11.1))=(20.91)/(1.11)=18.83 \end{gathered}`

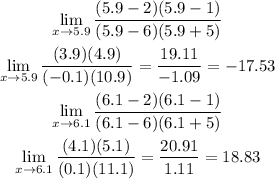
According to this, the limit approaches to negative infinity from the left (when x tends to 5.9 the limit is negative) and to positive infinity from the right (when x tends to 6.1 the limit is positive)