Since the time is in direct proportion with the length and inverse proportion with the number of workers, then
Let the amount of time is T, the length of the highway is L and the number of workers is N
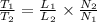
Since
T1 = 22, L1 = 24, N1 = 300
T2 = 33, L2 = 27, N2 = ?
Let us substitute them in the relation above
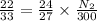
Let us simplify it
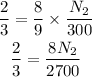
By using cross multiplication
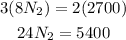
Divide both sides by 24
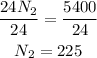
Then it needs 225 workers to finish the job