Question

(G.12, 1 point) Which point lies on the circle represented by the equation (X - 4)2 + (y - 2)2 = 722 O A. (-1, 4) O B. (8,3) O C. (9, 0) O D. (-2, 2)

Answer 1

We have a circle represented by the equation:

`(x-4)^2+(y-2)^2=7^2=49`

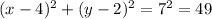
Any point that satisfy the equation of the circle lies in the circumference of the circle.

We can test each point by replacing the values of x and y in the equation by the coordinates of the point.

A) (-1,4)

`\begin{gathered} (-1-4)^2+(4-2)^2=49 \\ (-5)^2+2^2=49 \\ 25+4=49 \\ 29\\eq49 \end{gathered}`

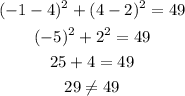
The point (-1,4) does not lie in the circle.

B) (8,3)

`\begin{gathered} (8-4)^2+(3-2)^2=49 \\ 4^2+1^2=49 \\ 16+1=49 \\ 17\\eq49 \end{gathered}`

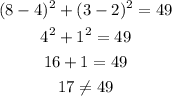
The point (8,3) does not lie in the circle.

C) (9,0)

`\begin{gathered} (9-4)^2+(0-2)^2=49 \\ 5^2+(-2)^2=49 \\ 25+4=49 \\ 29\\eq49 \end{gathered}`

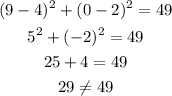
The point (9,0) does not lie in the circle.

D) (-2,2)

`\begin{gathered} (-2-4)^2+(2-2)^2=49 \\ (-6)^2+0^2=49 \\ 36+0=49 \\ 36\\eq49 \end{gathered}`

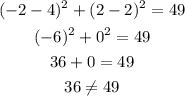
The point (-2,2) does not lie in the circle.