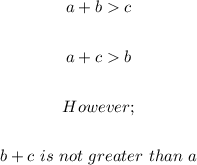Question

Determine the number of triangles that could be formed with the given measurements:Angle a= 50°, a = 17cm, b = 15cm

Answer 1

GIVEN:

We are given the following dimensions for a triangle ABC;

`\angle A=50\degree,a=17cm,b=15cm`

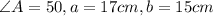
Required;

To determine the number of triangles that could be formed with the given measurements.

Step-by-step solution;

We will begin by identifying the measure of the unknown angle, which is angle B.

We shall apply the sine rule as follows;

`\begin{gathered} (a)/(sinA)=(b)/(sinB) \\ \\ (17)/(sin50\degree)=(15)/(sinB) \\ \\ Cross\text{ }multiply; \\ \\ sinB=(15)/(17)* sin50\degree \\ \\ sinB=0.675921567458 \end{gathered}`

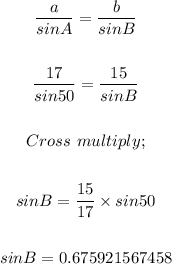
We now take the arc sin of the value of sine B and we'll have the degree measure as follows;

`\begin{gathered} sin^(-1)(0.675921567458)=42.5257561588 \\ \\ Rounded\text{ }to\text{ }the\text{ }nearest\text{ }tenth; \\ \\ B=42.5\degree \end{gathered}`

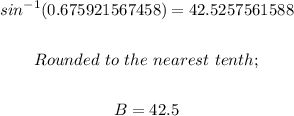
With these two angles, we can now determine angle C as follows;

`\begin{gathered} A+B+C=180\degree\text{ }(sum\text{ }of\text{ }angles\text{ }in\text{ }a\text{ }triangle) \\ \\ 50+42.5+C=180 \\ \\ 92.5+C=180 \\ \\ C=180-92.5 \\ \\ C=87.5\degree \end{gathered}`

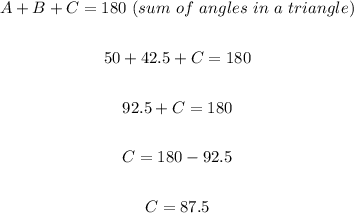
With this we can now determine the length of side c as follows;

`\begin{gathered} (a)/(sinA)=(c)/(sinC) \\ \\ (17)/(sin50)=(c)/(sin87.5) \\ \\ Cross\text{ }multiply; \\ \\ (17* sin87.5)/(sin50)=c \\ \\ 22.1708021244=c \\ \\ c\approx22.2\text{ }(Rounded\text{ }to\text{ }the\text{ }nearest\text{ }tenth) \end{gathered}`

We now have the dimensions of the sides and angles as follows;

`\begin{gathered} \angle A=50\degree,\angle B=42.5\degree,\angle C=87.5\degree \\ \\ a=50,b=15,c=22.2 \end{gathered}`

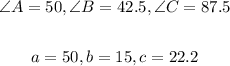
Therefore,

ANSWER:

We cannot form any triangle from the given measurements.

This is because for any given triangle, the sum of two sides must be greater than the third side.

Observe the following;

`\begin{gathered} a+b>c \\ \\ a+c>b \\ \\ However; \\ \\ b+c\text{ }is\text{ }not\text{ }greater\text{ }than\text{ }a \end{gathered}`