Step-by-step explanation
Since we have the △CDE,let's represent the triangle:
We can apply the law of sines to get the value of the angle C, and then by the Sum of Interior Angles of a Triangle Theorem, we can get the value of the angle D as shown as follows:
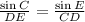
Substituting terms:
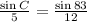
Isolating sin C:
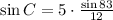
Applying sin^-1 to both sides:
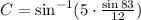
Computing the terms:
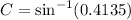
Computing the argument:
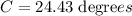
Finally, by applying the Sum of Interior Angles of a Triangle Theorem, we can get the value of D as shown as follows:
C + D + E = 180
24.43 + D + 83 = 180
Isolating D:
D = 180 - 83 - 24.43
Subtracting numbers:
D = 72.57 ≈ 72.6 degrees