Question

A rock is thrown from the side of a ledge. The height (in feet), x seconds after the toss is modeled by: h(x) = -3(x-2)2 +80 What is the maximum height that the rock reached?

Answer 1

The equation of the height of the rock is governed by:

`h(x)=-3(x-2)^2+80`

This is in the vertex form, which is:

`h(x)=a(x-b)^2+c`

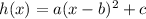
At x = b, the maximum value occurs and to find the actual maximum value, we plug in "b" into the function.

Now,

matching the vertex form with our equation, we see that:

b = 2 [thus, the maximum occurs at x = 2 seconds.

Let's find the max height by putting "2" into the equation:

`\begin{gathered} -3(2-2)^2+80 \\ =-3(0)^2+80 \\ =-3(0)+80 \\ =0+80 \\ =80 \end{gathered}`

The maximum height is 80 feet