Solution:
To find the area, A, ofa circular pond, we apply the formula to find thae area of a circle, which is
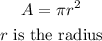
Given that the radius, r of the circua r pond is 8 ft
The area, A, of the circular pond will be
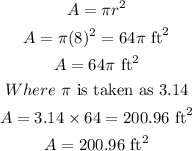
Where,
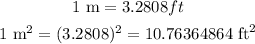
The area, A, of the circular pond in square meters will be
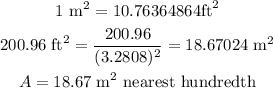
Hence, the answer is 18.67 m² (nearest hundredth)