Question

What is the y-intercept of a line that passes through the points (2, 7) and (6, 1

Answer 1

To find the y-intercept of the line, we must find the equation of the line

The form of the linear equation is

`y=mx+b`

m is the slope

b is the y-intercept

The rule of the slope is

`m=(y2-y1)/(x2-x1)`

Where (x1, y1) and (x2, y2) are two points on the line

Since the line passes through points (2, 7) and (6, 1), then

x1 = 2 and y1 = 7

x2 = 6 and y2 = 1

Substitute them in the rule above

`m=(1-7)/(6-2)=(-6)/(4)=-(3)/(2)`

Now put it in the form of the equation above

`y=-(3)/(2)x+b`

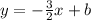
Now to find b substitute x and y in the equation by the coordinates of one of the 2 given point

Let us use point (2, 7)

x = 2 and y = 7

`\begin{gathered} 7=-(3)/(2)(2)+b \\ 7=-3+b \end{gathered}`

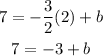
Add both sides by 3 to find b

`\begin{gathered} 7+3=-3+3+b \\ 10=b \end{gathered}`

B is the y-intercept, then

The y-intercept of the line is (0, 10)