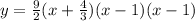Question

Determine an equation in factored form for the function shown below

Answer 1

The zeros pf the function are

`-(4)/(3)\text{ and 1}`

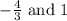
But since the curve hits the x -axis and bounces, it an extra zero of 1.

That means the function will be in the form

`y=a(x+(4)/(3))(x-1)(x-1)`

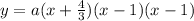
Note that the (x - 1) is reapeted.

Hence, it is a cubic function.

Since the y-intercept is 6, we set y to 6 and x to 0, and find a in the equation above, we have

`\begin{gathered} y=a(x+(4)/(3))(x-1)(x-1) \\ 6=a(x+(4)/(3))(x-1)(x-1) \\ 6=a(0+(4)/(3))(0-1)(0-1) \\ 6=a((4)/(3))(-1)(-1) \\ 6=(4)/(3)a \\ a=(6)/((4)/(3)) \\ a=(9)/(2) \end{gathered}`

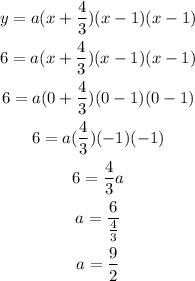
Hence, the answer is

`y=(9)/(2)(x+(4)/(3))(x-1)(x-1)`