In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
bag:
oranges and pears
# oranges = 3
p (oranges) = 0.2
Step 02:
probability:
p (event) = favorable outcomes / total outcomes
Event = orages:
# pears = p
favorable outcomes =e3
total outcomes = (# oranges + #pears) = (3 + p)

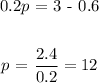
The answer is:
There are 12 pears i the bag