Question

Find the slope of a line parallel to the line through the points. (c) (10, 6) and (10, 10)

Answer 1

we are asked to determine the slope of a line that is parallel to the line that passes through the points (10,6) and (10,10). To do that, let's remember that the slopes of parallel lines are equal, therefore, we only need to find the slope of the first line. We find the slope using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where:

`\begin{gathered} (x_{1\text{,}}y_1)=(10,6) \\ (x_2,y_2)=(10,10) \end{gathered}`

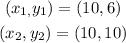
Replacing we get:

`m=(10-6)/(10-10)`

Solving the operations:

`m=(4)/(0)`

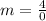
Since we get a division by zero, this means that the line is perpendicular to the x-axis and parallel the y-axis. Therefore, the slope of a parallel line to this is any line that is also perpendicular to the x-axis and parallel to the y-axis.