Question

I need help with number 1 written in black please

Answer 1

To find the piecewise function, let's divide the function into three parts:

Part 1: x ≤ -2

Part 2: -2 < x ≤ 3

Part 3: x ≥ 3

Now, let's find the function for each part.

Part 01:

As can be observed in the graph, for all the values of x ≤ -2 the output of the function is always y = 2.

So,

y = 2, if x ≤ -2

Part 02:

To find the equation of the line from part 02, let's choose two points.

Choosing points (0, 1) and (3, 4).

Given the equation of a line: y = mx + b, let's substitute the points to find m and b.

Substituting the point (0, 1):

`\begin{gathered} y=mx+b \\ 1=0m+b \\ 1=b \end{gathered}`

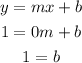
Then, y = mx + 1. Now, let's substitute the point (3, 4):

`\begin{gathered} y=mx+1 \\ 4=3m+1 \end{gathered}`

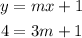
Subtracting 1 from both sides, then dividing both sides by 3:

`\begin{gathered} 4-1=3m+1-1 \\ 3=3m \\ (3)/(3)=(3)/(3)m \\ m=1 \end{gathered}`

The equation of the line is y = 1x + 1 or y = x + 1.

So,

y = x+1, if -2 < x ≤ 3

Part 03:

As can be observed in the graph, for all the values of x ≥ 3 the output of the function is always y =4.

So,

y = 4, if x≥3

Putting all together, the piecewise function is:

[tex]f(x)=\begin{cases}2,\text{ if }x\leq-2 \\ x+1,if\text{ }-2