Question

John decides to purchase a TV using an installment plan for the upcomingSuper Bowl. He needs to put 21% down on the $2,065 TV. Theremaining balance he would pay back over the next 3 years. The monthlypayments using the installment plan are $51.3. What is the financecharge? Round your answer to the nearest cent. Do not include a dollarsign in your answer.

Answer 1

Given that John puts down 21% on the $2065 TV, this implies that the initial amount paid on the TV is

`\begin{gathered} (21)/(100)*2065 \\ =\text{\$ }433.65 \end{gathered}`

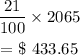
Thus, the remaining amount to be paid on the TV is

`\begin{gathered} \text{Remaining amount = 2065-433.65} \\ =\text{\$ }1631.35 \end{gathered}`

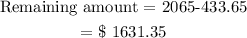
Given that the remaining balance is to be paid monthly using the installment plan at $51.3 for 3 years, this implies that

`\begin{gathered} \text{Amount paid installment for 3 years = 51.3}*\frac{3\text{ years}}{1\text{ year}}*12months \\ =\text{\$ 1846.8} \end{gathered}`

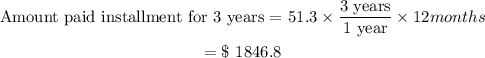
The finance charge on the TV is evaluated as the extra cost incurred when installmental payment is made as compared to outright payment.

In simple terms, it is the difference between the original remaining amount to be paid and the total amount paid in installment.

Thus,

`\begin{gathered} Finance\text{ charge = }1846.8-1631.35 \\ =215.45 \\ \Rightarrow Finance\text{ charge}\approx215.45\text{ (nearest cent)} \end{gathered}`

Hence, the finance charge on the TV is 215.45 (nearest cent).

`\text{ }`