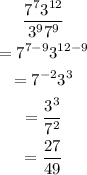The exponential to simplify is:
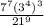
Let's use the property
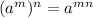
To simplify the numerator. So, we have:
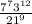
Now, let's use the property:
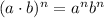
to simplify the denominator. Thus, we have:
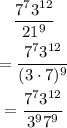
Now, we can cross-out numerator and denominator and simplify. The steps are shown below: