Question

A) Graph the system (Let M be represented by the horizontal axis and n be represented by the vertical axis)B) Find the solution to the system

Answer 1

Let's work on the following equation

`n=(2)/(3)m+5`

when m = 0,

`\begin{gathered} n=(2)/(3)\cdot0+5 \\ n=0+5 \\ n=5 \end{gathered}`

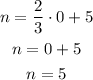
... n = 5

therefore, one of the points of this line is (0, 5)

let's find a second point

when n = 0, then

`\begin{gathered} 0=(2)/(3)\cdot m+5 \\ (2)/(3)m+5=0 \\ (2)/(3)m+5-5=0-5 \\ (2)/(3)m=-5 \\ 3\cdot(2)/(3)m=3\mleft(-5\mright) \\ 2m=-15 \\ (2m)/(2)=(-15)/(2) \\ m=-(15)/(2) \\ m=-7.5 \end{gathered}`

... m = - 7.5

therefore, the second point for this line is (-7.5 , 0)

using this two points we can graph the system

so, the graph for the equation n = 2/3 m + 5 will be:

The second equation is:

`6m-9n=-45`

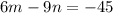
Again, let's find two points tha belong to the line

when m = 0, then

`\begin{gathered} 6\cdot0-9n=45 \\ 0-9n=-45 \\ -9n=-45 \\ n=(45)/(9) \\ n=5 \end{gathered}`

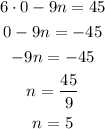
... n = 5

So, our first point for this equation, is (0. 5)

for our second point, when n = 0, then

`\begin{gathered} 6m-9\cdot0=-45 \\ 6m-0=-45 \\ 6m=-45 \\ m=(-45)/(6) \\ m=-7.5 \end{gathered}`

... m = -7.5

Therefore, the second point is (-7.5 , 0)

This equation can be represented by the following graph:

Finally, we need to solve the system of equations

`\begin{gathered} n=(2)/(3)m+5 \\ 6m-9n=-45 \end{gathered}`

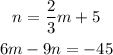
substite n from eq1 to eq2

`6m-9\mleft((2)/(3)m+5\mright)=-45`

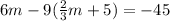
simplify

`\begin{gathered} 6m-(9\cdot2)/(3)m-(9\cdot5)=-45 \\ 6m-6m-45=-45 \\ 0-45=-45 \\ -45=-45 \end{gathered}`

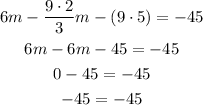
Since we obtained -45 = -45, the system of equations has infinite solutions