Question

If y varies directly as x2 and y=290 when x=12, find y if x=18. (Round off your answer to the nearest hundredth.)

Answer 1

We know that y varies directly as x². This can be expressed as:

`y=k\cdot x^2`

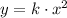
where k is the constant of proportionality.

We know that y = 290 when x = 12.

We can find the value of k replacing x and y with the values:

`\begin{gathered} y=k\cdot x^2 \\ k=(y)/(x^2) \\ k=(290)/(12^2) \\ k=(290)/(144) \\ k=(145)/(72) \end{gathered}`

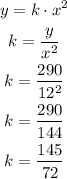
We then can calculate the value of y when x = 18 as:

`\begin{gathered} y=(145)/(72)x^2 \\ y=(145)/(72)\cdot(18^2) \\ y=(145)/(72)\cdot324 \\ y=652.5 \end{gathered}`

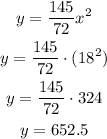
Answer: y = 652.5