Question

Which is the graph of the equation y-1= 1= (x-3)? у 8 4 . -10-3 A-22 3 6

Answer 1

First of all, we need to write the equation given:

`y-1=(2)/(3)(x-3)`

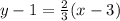
We solve that equation to y like this:

`\begin{gathered} y-1=(2)/(3)(x-3) \\ y=(2)/(3)x-3\cdot(2)/(3)+1 \\ y=\text{ }(2)/(3)x-2+1 \\ y=\text{ }(2)/(3)x-1 \end{gathered}`

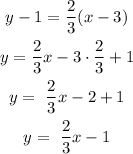
To draw that we need to find two points and make a line join together those poins.

We start to x=0, like this:

`\begin{gathered} y=\text{ }(2)/(3)x-1;\text{ x=0} \\ y=(2)/(3)(0)-1 \\ y=-1 \end{gathered}`

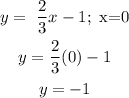
Then the first point is (0,-1)

For the second point we make y = 0, then:

`\begin{gathered} y=(2)/(3)x-1;\text{ y=0} \\ 0=(2)/(3)x-1 \\ 1=(2)/(3)x \\ (3)/(2)=x=1.5 \end{gathered}`

Now, the second point will be (3/2,0)

Finally, we put that on a graph and compare with your options...

That will be the draw.. and from your options...