the sequence given is 2, 8, 32 128, .....
the first term = 2
common ratio = the ratio between two successive term we can pick either the 3rd term from the 4th term
the general formula of recursive formula is
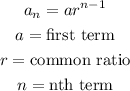
to find the common ratio
we can use the ratio between two successive terms
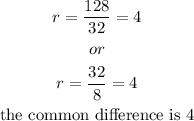
now, we'll proceed to find the recursive formula
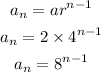
the answer is option b