Question

The data in the table the number of boys b and girls g in several different classes. Find the correlation coefficient and the equation of the line of best fit for the data. Treat the number of girls in the classes as the independent variable.

Answer 1

The correlation coefficient is given by the formula:

x is the independent variable (number of girls) and y is the dependent variable (number of boys). With the shared values, let's find the terms of the formula, as follows:

n is the number of data, so n=9. By replacing these values into the formula, we obtain r:

`\begin{gathered} r=((9*2369)-(158*140))/(√([9*3448-(158)^2][9*2520-(140)^2])) \\ \\ r=(21321-22120)/(√([6068][3080])) \\ \\ r=(-799)/(4323.13) \\ \\ r\approx-0.18 \end{gathered}`

The correlation coefficient is approximately -0.18.

The equation of the line of best fit is given by:

`\hat{y}=a+bx`

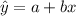
Where b is the slope and a is the y-intercept. The formulas give these:

`\begin{gathered} b=(n\sum xy-(\sum x)(\sum y))/(n\sum x^2-(\sum x)^2) \\ \\ a=(\sum y-b\sum x)/(n) \end{gathered}`

We calculated these values in the last step, so, let's replace them and solve for a and b:

`\begin{gathered} b=(9*2369-158*140)/(9*3448-(158)^2)=(21321-22120)/(6068)=(-799)/(6068)=-0.13 \\ \\ a=(140-(-0.13)(158))/(9)=(140+20.54)/(9)=(160.54)/(9)=17.9 \end{gathered}`

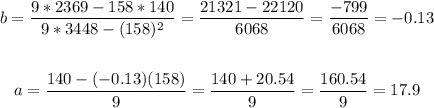
Then, as y=boys and x=girls, then the line of best fit will be:

`b=-0.13g+17.9`

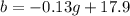
The answer is r=-0.18 and b=-0.13g+17.9