Question

The time T, in seconds, it takes a pendulum to make one swing depends on the length of the pendulum and is given byT(L) = 2 L32where L is the length of the pendulum in feet.(a) Find the time (in seconds) it takes the pendulum to make one swing if the length of the pendulum is 6 ft. Round to the nearest hundredth of a second.________ sec(b) Find the time it takes (in seconds) the pendulum to make one swing if the length of the pendulum is 9 in. Round to the nearest tenth of a second.________ sec

Answer 1

The expression of the time taken to swing the pendulum is,

`T(L)=2\pi\sqrt[]{(L)/(32)}`

Part (a)

Substitute the known values in the expression of time.

`\begin{gathered} T(L)=2(3.14)\sqrt[]{(6)/(32)} \\ =(6.28)(0.433) \\ \approx2.72\text{ s} \end{gathered}`

Thus, the time taken by pendulum to complete one swing is 2.72 s.

Part (b)

Convert the length of pendulum in feet as,

`\begin{gathered} 9\text{ in=}(9\text{ in)(}\frac{1\text{ ft}}{12\text{ in}})_{} \\ =0.75\text{ ft} \end{gathered}`

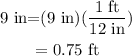
Substitute the known values in the expression of time.

`\begin{gathered} T(L)=2(3.14)\sqrt[]{(0.75)/(32)} \\ =(6.28)(0.153) \\ \approx1.0\text{ s} \end{gathered}`

Thus, the time taken by pendulum to complete one swing is 1.0 s.