We know that Conner rakes the front lawn in 15 hours, this means that Conner's rate is:
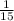
On the other hand, Devante does the work in 9 hours then his rate is:
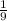
Let x be the time if they do the work together, then their rate is:

Hence the sum of their individual rates is equal to the combined rate:
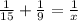
Solving for x we have:
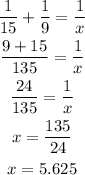
Therefore, the time it takes them 5.625 hours to do the job together.