Question

N the diagram below, segment PB is a tangent. IF AC = 45 and PA = 4, find PB.

Answer 1

Given that segment PB is a tangent, you can identify that segment PC is secant.

You know that:

`\begin{gathered} AC=45 \\ PA=4 \end{gathered}`

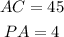
According to the Intersecting Secant-Tangent Theorem:

`Tangent=\sqrt{Secant\text{ }segment\cdot External\text{ }secant\text{ }segment}`

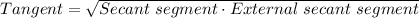
In this case, you can identify that:

`Secant\text{ }segment=PC=PA+AC=4+45=49`
`External\text{ }secant\text{ }segment=PA=4`

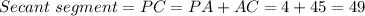
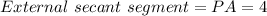
Therefore, you can determine that:

`\begin{gathered} PB=√(49\cdot4) \\ PB=14 \end{gathered}`

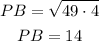
Hence, the answer is: Option b.