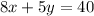Question

OCWhich of the following equations does the graph below represent?

Answer 1

8x + 5y = 40

Step-by-step explanation

We can see in the graph that the line intersects the y-axis at y = 8. When we have the equation of a line in the form:

`ax+by=c`

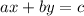
The y-intercept is the quotient:

`y_{\text{ intercept}}=(c)/(b)`

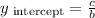
If the y-intercept is 8 and the intependent term is 40, then the coefficient of y must be 5. So b = 5:

`ax+5y=40`

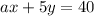
The slope of the line, with the given form of the equation is:

`m=-(a)/(b)`

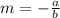
We can see in the graph that the slope is -8/5. Therefore, if b = 5, then a = 8.

Hence, the equation that represents the graph is:

`8x+5y=40`