Given: A triangle ABC with altitude BD=6.5 units and side AB=7.5 units, BC=10 units.
Required: To determine the length of AC.
Explanation: The triangle ABD and triangle BCD are right-angled triangles. Hence we can apply Pythagoras theorem which states that

Hence for triangle ABD, we can write
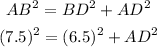
or,

Similarly, for triangle BCD, we have
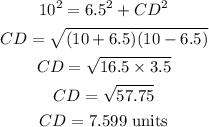
Now,
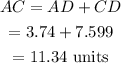
Final Answer: The length of AC is 11.34 units.