Question

A. rubber-wheeled 50k cart rolls down a 15-degree incline. What is the cart's acceleration of rolling friction is (a) neglected and (b) included?

Answer 1

(a) a = 2.54 m/s²

(b) a = 2.35 m/s²

Step-by-step explanation:

The situation can be modeled with the following free body diagram.

Part (a)

If the rolling friction is neglected, the net force will be the component of the weight that is parallel to the incline, and by the second law of Newton, we get:

`F_{\text{net}}=mg\sin 15=ma`

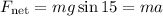
So, solving for a and replacing the values, we get:

`\begin{gathered} mg\sin 15=ma \\ g\sin 15=a \\ a=(9.8m/s^2)(\sin 15) \\ a=2.54m/s^2 \end{gathered}`

Part (b)

If the rolling friction is included, we first need to calculate the normal force. Since there is no net force in the perpendicular direction of the incline, we get:

`\begin{gathered} Fn=mg\cos (15) \\ Fn=(50kg)(9.8m/s^2_{})\cos (15) \\ F_n=473.30\text{ N} \end{gathered}`

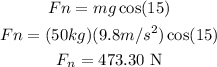
Then, taking into account that the rolling coefficient between the rubber and the concrete is 0.02, we get that the rolling friction is equal to:

`\begin{gathered} F_f=\mu F_n \\ F_f=\text{0}.02(473.3N) \\ F_f=9.47N \end{gathered}`

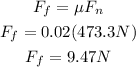
Finally, the net force is equal to

`\begin{gathered} F_{\text{net}}=mg\sin (15)-F_f=ma \\ \longrightarrow a=(mg\sin (15)-F_f)/(m) \end{gathered}`

Replacing the vales, we get:

`\begin{gathered} a=((50kg)(9.8m/s^2)\sin(15)-9.47N)/(50kg) \\ a=2.35m/s^2 \end{gathered}`

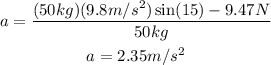
Therefore, the acceleration when the friction is neglected is 2.54 m/s², and the acceleration when the friction is included is 2.35 m/s²