Question

Which value of x is a solution to this equation ? 2x² + 5x - 63 =0A) 9B)3C) -7D)-4

Answer 1

Hello!

We have the equation 2x² +5x -63 = 0

First, let's find the coefficients a, b and c as ax² +bx +c = 0:

• a = 2

,

• b = 5

,

• c = -63

Now, we will use the formula below to solve this equation:

`x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}`

Let's replace the coefficients with the values that we already found:

`\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4\cdot2\cdot(-63)_{}}}{2\cdot2} \\ \\ x=\frac{-5\pm\sqrt[]{5^2+504_{}}}{4} \\ \\ x=\frac{-5\pm\sqrt[]{25^{}+504_{}}}{4} \\ \\ x=\frac{-5\pm\sqrt[]{529}}{4} \\ \\ x=(-5\pm23)/(4) \end{gathered}`

Now, let's divide it into two solutions, look:

`\begin{gathered} x_1=(-5+23)/(4)=(18)/(4)=(9)/(2) \\ \\ x_2=(-5-23)/(4)=-(28)/(4)=-7 \end{gathered}`

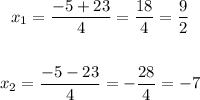
Right answer: C) -7 is a solution.