Solution:
Given that the railroad's track is determined using the graph below:
and the highway's path can be found using the equation:
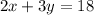
To determine the intersection, we plot the graph of the highway's path.
To plot the graph, we solve for y for various values of x.
Thus, we have
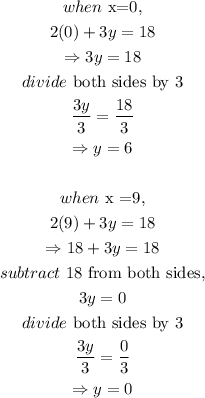
By plotting the x and y values as points (x, y) on a graph, we have
From the graphs, we can conclude there are no intersections between the railroad and the highway