Question

The values of x shown on the number line below are solutions to an absolute valueequation.

Answer 1

We will use the solutions to the absolute value functions to determine the function's description as follows:

The two solutions to the absolute value function are given as follows:

`x\text{ = -3 and x = 5}`

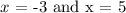
We will investigate each description as follows:

A) The distance of x from -3 is 8.

We will use the number line and determine the distance from ( x = -3 ) to the other solution ( x = 5 ). The number of units along the x-axis from point ( x = -3 ) to ( x = 5 ) would be:

`\textcolor{#FF7968}{8}\text{\textcolor{#FF7968}{ units}}`

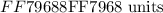
Hence, option A is correct!

B) This option describes the absolute value function as follows:

`|\text{ x }-\text = 5`

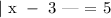
We will solve the above absolute value function as follows:

`\begin{gathered} +(x\text{ - 3 ) = 5 OR -(x - 3 ) = 5} \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 8 }}\text{ OR }\text{\textcolor{#FF7968}{x = -2}} \end{gathered}`

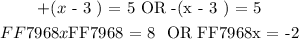
The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option B is incorrect!

C) The distance of x from 1 is 4

The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 1 ) as follows:

`\text{\textcolor{#FF7968}{Distance}}\text{ = 5 - 1 = 1 - ( - 3 ) = 4}`

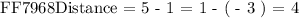
We see that the distance from each solution ( x = -3 ) AND ( x = 5 ) from point ( x = 1 ) is 4 units along the x axis. Hence, option C is correct!

D) The distance of x from 4 is 1

The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows:

`\begin{gathered} \text{Distance : ( x = 5 ) - ( x = 4 ) = }\text{\textcolor{#FF7968}{1 unit}} \\ \text{Distance : ( x = -3 ) - ( x = 4 ) = }\text{\textcolor{#FF7968}{7 units}} \end{gathered}`

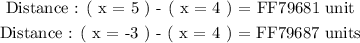
The above statement is true for the solution ( x = 5 ); however, incorrect for solution ( x = -3 ). Hence, we will reject this option D as it is not true in entirety!

E) This option describes the absolute value function as follows:

`|\text{ x }-\text 4 1`

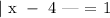
We will solve the above absolute value function as follows:

`\begin{gathered} +(x\text{ - 4 ) = 1 OR - ( x - 4 ) = }1 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 5 }}\text{ OR }\text{\textcolor{#FF7968}{x = }}\textcolor{#FF7968}{3} \end{gathered}`

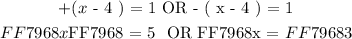
The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option E is incorrect!

F) This option describes the absolute value function as follows:

`|\text x + 1 4`

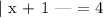
We will solve the above absolute value function as follows:

`\begin{gathered} +(x\text{ + 1 ) = 4 OR - ( x + 1 ) = }4 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 3 }}\text{ OR }\text{\textcolor{#FF7968}{x = -}}\textcolor{#FF7968}{3} \end{gathered}`

The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option F is incorrect!

G) The distance of x from -3 is 5

The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows:

`\begin{gathered} \text{Distance : ( x = 5 ) - ( x = -3 ) = }\text{\textcolor{#FF7968}{8 unit}} \\ \end{gathered}`

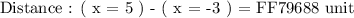
The above statement is not true for the solution ( x = 5 ). Hence, we will reject this option G as it is not true in entirety!

H) This option describes the absolute value function as follows:

`|\text{ x }-\text 1 4`

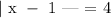
We will solve the above absolute value function as follows:

`\begin{gathered} +(x\text{ - 1 ) = 4 OR - ( x - 1 ) = }4 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 5 }}\text{ OR }\text{\textcolor{#FF7968}{x = -}}\textcolor{#FF7968}{3} \end{gathered}`

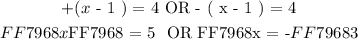
The above solution to the absolute value function is equal to the solution presented in the number line. Hence, option H is correct!

The correct statements are:

`\textcolor{#FF7968}{A}\text{\textcolor{#FF7968}{ , C , H}}`

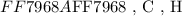
The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows: