Question

Determine the celsius temperature of 2.49 mol of a gas contained in a 1.00 L vessel at a pressure of 143 kPa

Answer 1

Answer: the temperature of the gas under the conditions given is -266°C

Step-by-step explanation:

The question requires us to determine the temperature of a gas, in Celsius degrees, knowing that there are 2.49 moles of the gas contained in a 1.00 L vessel at a pressure of 143 kPa.

To solve this problem, we can apply a rearranged equation of ideal gases, as shown below:

`P* V=n* R* T\rightarrow T=(P* V)/(n* R)`

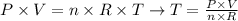
where P is the pressure of the gas, V is the volume of the gas, n is the number of moles and R is the constant of gases.

Since the question did not provide a value for R, we'll apply 8.314 kPa.L/K.mol. Note that the temperature will be obtained in Kelvin, and we'll need to convert it to Celsius degrees.

Applying the values provided by the question, we'll have:

`\begin{gathered} \begin{equation*} T=(P* V)/(n* R) \end{equation*} \\ T=((143kPa)*(1.00L))/((2.49mol)*(8.314kPa.L.K^(-1).mol^(-1)))=6.91K \end{gathered}`

Therefore, the temperature of the gas is 6.91K.

We can convert this temperature to °C as it follows:

`\begin{gathered} K=°C+273.15\rightarrow°C=K-273.15 \\ T(°C)=6.91-273.15=-266°C \end{gathered}`

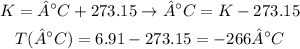
Therefore, the temperature of the gas under the conditions given is -266°C.