Question

What is the value of (x - y) (x - y) if xy = 12 and x² + y² = 25?

Answer 1

`\begin{gathered} xy=12 \\ x^2+y^2=25 \end{gathered}`

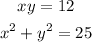
In order for us to determine the value of (x - y)(x - y), we have to solve for the value of x and y first. To do that, we can use the substitution method. Here are the steps.

1. Rewrite equation 1 xy = 12 in terms of "y" by dividing both sides of the equation by x.

`(xy)/(x)=(12)/(x)\Rightarrow y=(12)/(x)`

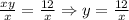
So, equation 1 becomes y = 12/x.

2. Replace the value of y in equation 2 with 12/x.

`\begin{gathered} x^2+y^2=25 \\ x^2+((12)/(x))^2=25 \end{gathered}`

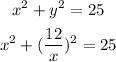
Then, solve for x.

`x^2+(144)/(x^2)=25`

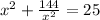
Add the terms on the left side of the equation. Use x² as the GCD.

`(x^4+144)/(x^2)=25`

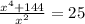
Cross multiply.

`\begin{gathered} x^4+144=25x^2 \\ x^4-25x^2+144=0 \end{gathered}`

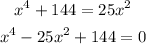
Then, we factor the quartic polynomial. In order to factor, just answer the question "what are the factors of 144 that add to -25?".

The factors are -16 and -9. Hence, we can rewrite the equation as:

`x^4-16x^2-9x^2+144=0`

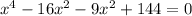
Then, divide the equation into two groups.

`(x^4-9x^2)-(16x^2-144)=0`

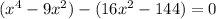
Then, factor out x² in the first group and factor out 16 in the second group.

`x^2(x^2-9)-16(x^2-9)=0`

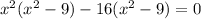
Since x² - 9 is a common factor on both groups, we can just rewrite it as:

`(x^2-16)(x^2-9)=0`

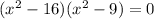
Then, equate each factor to zero. Then, solve for x.

`\begin{gathered} x^2-16=0 \\ x^2=16 \\ x=\pm4 \end{gathered}`
`\begin{gathered} x^2-9=0 \\ x^2=9 \\ x=\pm3 \end{gathered}`

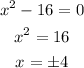
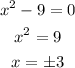
Therefore, there are 4 possible values of x. These are +4, -4, +3, and -3.

Since xy = 12, then:

1. At x = 4, y = 3.

2. At x = -4, y = -3.

3. At x = 3, y = 4.

4. At x = -3, y = -4.

Let's plug the pairs of x and y in the expression (x - y)(x - y) and solve.

`\begin{gathered} 1.\text{ }(4-3)(4-3)=(1)(1)=1 \\ 2.\text{ }(-4--3)(-4--3)=(-1)(-1)=1 \\ 3.\text{ }(3-4)(3-4)=(-1)(-1)=1 \\ 4.\text{ }(-3--4)(-3--4)=(1)(1)=1 \end{gathered}`

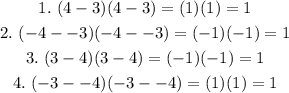
On all pairs, the value of (x - y)(x- y) is 1. Hence, the answer is 1.