SOLUTION
To solve this, we get the Z for 81 and 89
We will use the formula

Z for 81, we have
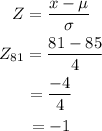
Z for 89, we have
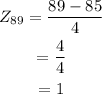
Using the Zscore calculator for probability between two Zscores, we have
[tex]P(-1
Hence the answer is 0.68 to the nearest hundredth
Or 68.27% to the nearest hundredth