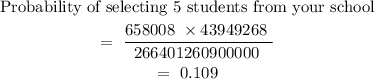Step 1
Ways to choose 5 from 40 multiplied by ways to choose 5 from the other 90 and number of ways to choose 10 in all from 130 as the denominator
Step 2:
Apply combination formula
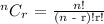
Step 3:
Ways to choose 5 from 40

Step 4
ways to choose 5 from the other 90
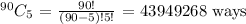
Step 5
ways to choose 10 in all from 130
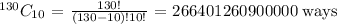
Step 6
Ways to choose 5 from 40 multiplied by ways to choose 5 from the other 90 and number of ways to choose 10 in all from 130 as the denominator