We are asked to determine the amount of work requiere to pump all the water from the top of the cone. To do that we will use the following formula for work:
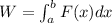
Where:
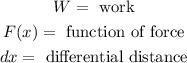
To do this we need to set a coordinate system at the bottom of the cone, like this:
We have taken a differential segment of the volume of water to study the behavior of the system.
Now, according to Newton's second law, the force is given by:
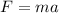
Where "m" is mass and "a" is acceleration". The mass is equivalent to the product of the density and the volume, like this:
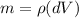
Where:
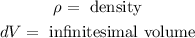
Now, we substitute in the formula for the force:
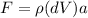
The acceleration is the acceleration due to gravity which symbol is "g":
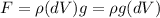
The product of the density and the acceleration of gravity is the weight density and in this case, is a constant value of 2 N/cm^3. Substituting the value we get:
![F=(2\frac{N}{\operatorname{cm}^3})dV]()
Now, we need to determine the infinitesimal segment of volume. We do that using the following:
The infinitesimal segment is approximately equal to a disc with a height of "dx", therefore, its volume is:
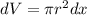
The radio "x" varies with the value of "x". We can determine this variation using similarities between the right triangles formed by the cone and the level of water, like this:
using similarities of triangles we get:
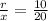
Simplifying:
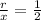
Now, we multiply both sides by "x":
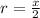
Now, we substitute the formula for the radius in the formula for the infinitesimal volume:
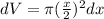
Now, we need to determine the distance the segment will move. We notice that the distance the segment moves is:
Therefore, the distance moves is equivalent to "20 - x". Now, we substitute in the formula for work:
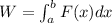
We plug in the formulas for the force and the distance:
![W=\int ^b_a(2\frac{N}{\operatorname{cm}^3})\pi((x)/(2))^2(20-x)dx]()
Now, we simplify, by taking out the constant values and solving the square:
![W=(2\frac{N}{\operatorname{cm}^3})(\pi)/(4)\int ^b_ax^2(20-x)dx]()
Now, the limits of integration must be the values of "x" where there is water. That is from the bottom of the cone until the value of "h". Therefore, we have;
![W=(2\frac{N}{\operatorname{cm}^3})(\pi)/(4)\int ^(18)_0x^2(20-x)dx]()
Now, we apply the distributive law inside the integral:
![W=(2\frac{N}{\operatorname{cm}^3})(\pi)/(4)\int ^(18)_0(20x^2-x^3)dx]()
Now, we integrate:
![W=(2\frac{N}{\operatorname{cm}^3})(\pi)/(4)((20x^3)/(3)-(x^4)/(4))^(18)_0]()
Now, we substitute the limits of integration:
![W=(2\frac{N}{\operatorname{cm}^3})(\pi)/(4)((20(18)^3)/(3)-((18)^4)/(4)^{}_{})]()
Solving the operations we get:
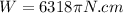
Now, we convert the centimeters into meters to get the answer is Joules:
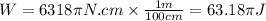
Therefore, the amount of work required is 63.18pi Joules