You have the following information:
- The length of the given rectangle is 3 inches shorter than twice the width x.
- The area of the rectangle is 1377 square inches
In order to determine the width of the rectangle, you first name x as the width of the rectangle. Thus the length of th rectangle is 2x - 3 (3 inches shorter than twice the width). The area (which is equal to 1377 square inches) is given by the product beteen the length and the width.
Then, for the are of the rectangle you have:
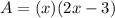
You replace the value of A in the previous expression and order the equation to obtain a quadratic equation, just as follow:
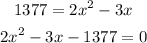
To solve the previous equation for x, you use the quadratic formula, which is given by:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
where a=2, b=-3 and c=-1377. You replace and obtain:
![\begin{gathered} x=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(2)(-1377)}}{2(2)} \\ x=\frac{3\pm\sqrt[]{9+11,016}}{4}=(3\pm105)/(4) \\ x_1=27 \\ x_2=-25.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rkn2nmy3rxyi06fbx7w2hm6u5hmbi4dm27.png)
There are two solutions because we had a quadratic equations. However, from the two solutions found you can only take x1 = 27, because this solution is positive and it has physical sense.
Hence, the width of the rectangle is 27 inches