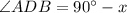Solution:
(a) In the given figure,
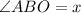
BD is the bisector of angle ABC, thus:
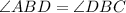
So, write as follows:
(i)
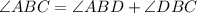

Therefore,
![\operatorname{\angle}ABC=2x]()
(ii)
OB=OA=OD radii of the same circle.
As OB=OA then in triangle AOB,
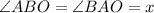
BOD is a diameter of a circle. then by theorem of circle,
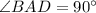
thus,
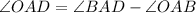

OA=OD , in the tringle AOD,
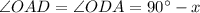
In triangle AOD,
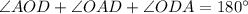
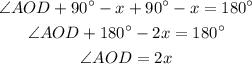
Therefore,
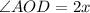
(iii) By the theorem of circle, the angle formed at the center of the circle is twice the angle formed at the circumference of the circle with the same base.

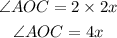
Therefore,
![\operatorname{\angle}AOC=4x]()
(iv)
OA=OD , thus tringle AOD is an isosceles triangle,
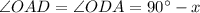
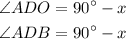
Therefore,