1) According to the rational root theorem, the roots of the function are given by p/q, where p is a factor of a_0 and q is a factor of a_n. In our case,
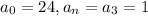
Thus, the possible roots are
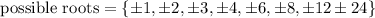
We need to test each option,
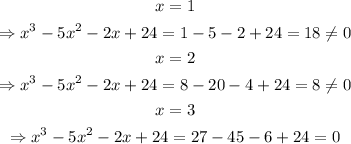
Thus, a root of the equation is x=3; then,
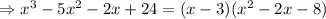
Finally, we can easily factorize the quadratic term,
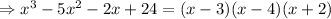
The answer to question 1) is (x-3)(x-4)(x+2).
2) Given the initial equation,
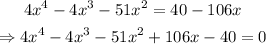
Using the same theorem as in part 1)
The possible roots are
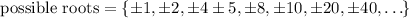
Testing the options,
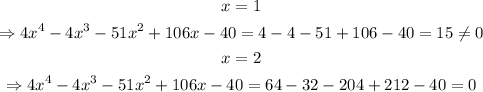
Then, a root of the equation is x=2; thus,
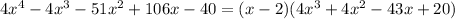
Using the Rational Root theorem on the cubic term,
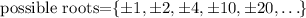
Testing each option,
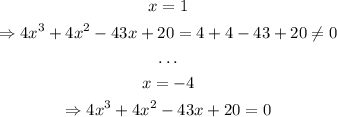
Thus,
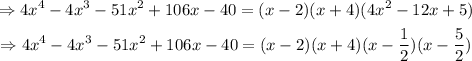
Where
![\begin{gathered} 4x^2-12x+5=0 \\ \Rightarrow x=\frac{-(-12)\pm\sqrt[]{(-12)^2-4\cdot4\cdot5}}{2\cdot4}=\frac{12\pm\sqrt[]{64}}{8}=(12\pm8)/(8) \\ \Rightarrow x=(20)/(8),x=(4)/(8) \\ \Rightarrow x=(5)/(2),x=(1)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x0ox27bzn80fitqbcuvjf4f1o8c2y1uwnp.png)
Therefore, the answer to part 2) is (x-2)(x+4)(x-1/2)(x-5/2)
c) Given the equation
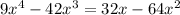
Then,
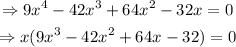
Using the Rational root theorem on the cubic part,
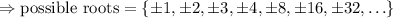
Testing each possibility until finding a root,
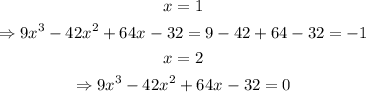
Thus,
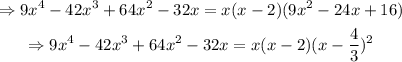
The answer to part c) is x(x-2)(x-4/3)^2