Question

A positive charge of 0.038 C moves horizontally to the right at a speed of 312.869 m/s and enters a magnetic field directed vertically downward. If it experiences a force of 40.356 N, what is the magnetic field strength ?

Answer 1

The magnitude F of the force experienced by a charged particle with charge q moving perpendicular to a magnetic field B with a speed v is given by:

`F=qvB`

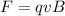
Since the charge moves horizontally to the right and the magnetic field is directed vertically downward, then the movement of the charge and the direction of the magnetic field are perpendicular.

The charge, the speed and the magnitude of the force are given in the problem, so the only unknown in the equation is B. Isolate B from the equation and replace F=40.356N, v=312.869m/s and q=0.038C to find the strength of the magnetic field:

`\begin{gathered} F=qvB \\ \\ \Rightarrow B=(F)/(qv)=(40.356N)/((0.038C)(312.869(m)/(s)))=3.394391902...T \\ \\ \therefore B\approx3.4T \end{gathered}`

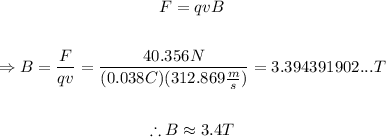
Since the quantity with less significant figures is the charge and it has 2 significant figures, then, the result must have a maximum of 2 significant figures.

Therefore, the strength of the magnetic field is approximately 3.4 Teslas.