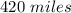You know that:
- Last weekend his trip took 10 hours when he drove to the mountains.
- When he drove home, the trip took 7 hours.
- His average rate was 18 miles per hour faster on the trip home.
By definition, the distance can be calculated with this formula:
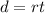
Where "d" is distance, "r" is rate, and "t" is time.
Then, you can set up the following equation to represent his trip to the mountains ("d" is in miles):
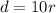
And you can set up the following equation to represent his trip home ("d" is in miles):
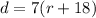
To find the value of "r", you need to make both equations equal to each other and solve for "r". Then, you get:
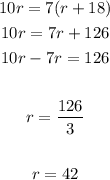
Knowing the value of "r", you can substitute it into the second equation:
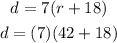
Finally, evaluating, you get (Remember that "d" is in miles)
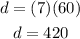
Therefore, the answer is: