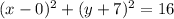Given the equation of the circle:
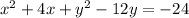
We will complete the squares for x and y to write the equation of the circle as:
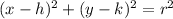
Where (h,k) is the coordinates of the circle and r is the radius of the circle
so, the equation will be:
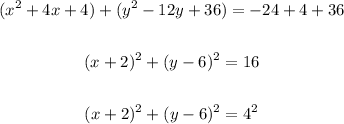
So, the radius of the circle = 4
And the center of the circle = ( -2, 6 )
Now, we will make the transformation for the circle:
Shift 1 unit up, the center will be = ( -2, 7 )
shift 2 units right, the center will be = ( 0, 7 )
Reflection across the x-axis, the center will be = ( 0, -7)
So, the equation of the circle after transformation will be:
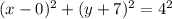
So, the answer will be: