Question

What’s the potential and kinetic energy when it’s halfway down the hill?

Answer 1

According to the Law of Conservation of Mechanical Energy, if there are no external or non-conservative forces acting on a system (such as friction), then, the total mechanical energy of the system remains constant.

The mechanical energy of a system is the sum of its kinetic energy K and its potential energy U:

`E=K+U`

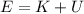
The kinetic energy of a particle with mass m and speed v is:

`K=(1)/(2)mv^2`

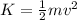
And the potential energy of a particle with mass m located at a height h is:

`U=mgh`

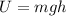
Where g is the acceleration of gravity on the surface of Earth.

When the roller coaster car is located at the top of the 30.00-meter hill, its kinetic energy is 0 and its potential energy is:

`U_1=(2500kg)(9.8(m)/(s^2))(30.00m)=735,000J`

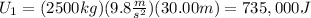
Then, the total mechanical energy of the roller coaster car is:

`E=U_1+K_1=735,000J+0J=735,000J`

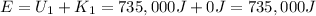
On the other hand, the potential energy of the car when it is halfway down is:

`U_2=(2500kg)(9.8(m)/(s^2))(15.00m)=367,500J`

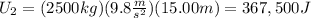
Since the total mechanical energy is the same, we can find the kinetic energy of the car when it is halfway down using the law of conservation of mechanical energy:

`\begin{gathered} E=U_2+K_2 \\ \\ \Rightarrow K_2=E-U_2=735,000J-367,500J=367,500J \end{gathered}`

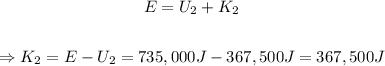
Therefore, the potential and kinetic energy of the car when it is halfway down the hill at a height of 15.0 meters are:

`\begin{gathered} U_2=367,500J \\ K_2=367,500J \end{gathered}`

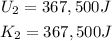
Using PE for potential energy and KE for kinetic energy:

`\begin{gathered} PE=367,500J \\ KE=367,500J \end{gathered}`

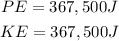
Therefore, the correct choice is the second option.